배열?
- 배열은 연속된 자료를 저장하기 위한 선형 자료 구조다
- 배열은 기본적으로 지역적 특성을 가지고 있기 때문에 CPU가 지역 참조를 할 때 속도가 빠르다
- 다시말해서, Cache Hit 의 가능성이 커진다!
- 우리는 이미 배열을 사용하는 법 을 알고 있다!! But.... new int[1000] 는 한계성이 있다.
* 입력으로 들어오는 개수가 N(미지수)일 때, 어떠한 근거로 메모리를 확보해야 되는가? 에 대한 문제점
--> 정적 배열을 동적 배열로 사용하면 된다!! -> ArrayList
ArrayList?

- 배열의 크기를 들어오는 자료의 양에 따라서 조절할 수 있다!!
- 데이터를 추가하는 데에 시간복잡도는 O(1) 에 처리할 수 있다
▶ 하지만....
- 동적으로 메모리가 늘어나는 것처럼 보이기 위해 어떤 식으로 메모리를 늘린다는 말인가?
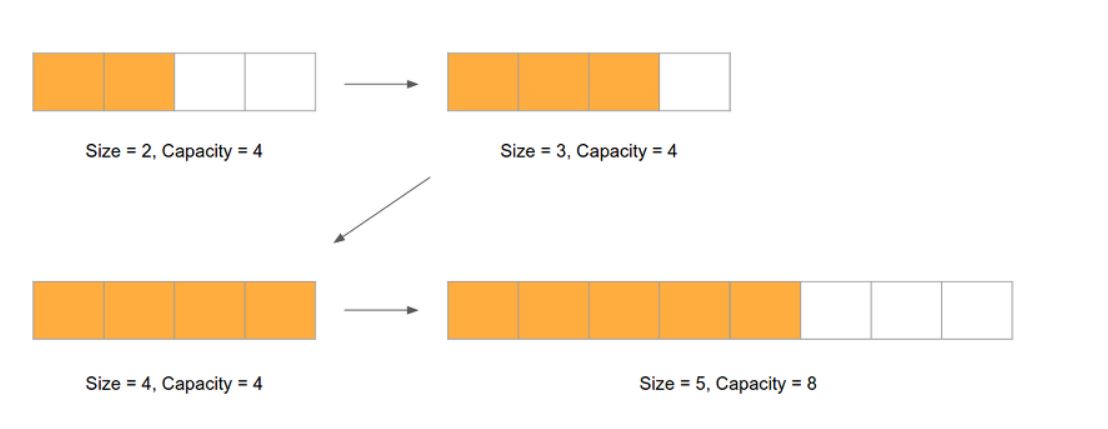
- 배열의 초기 Size와 Capacity는 1로 지정한다!
- 그 다음, 배열의 크기를 늘리는 기준은 ( 기존 배열의 크기 ) * 2 로 늘린다!!
EX) 배열의 크기(Size)가 2, 용량(Capacity)가 2일 때,, 원소를 추가하게 되면
Capacity가 4인 배열을 만들고, Arrays.copy() 메서드를 이용하여 데이터를 복사한다. -> 시간복잡도 O(N)
- ArrayList의 메모리 늘리는 기준은 ( 기존 배열의 크기 ) * 1.5
int oldCapacity = elementData.length;
int newCapacity = oldCapacity + (oldCapacity >> 1);
if (newCapacity - minCapacity < 0)
newCapacity = minCapacity;
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
// minCapacity is usually close to size, so this is a win:
elementData = Arrays.copyOf(elementData, newCapacity);
[ Why??? ]
- 추가하는데에 걸리는 시간복잡도를 평균적으로 O(1)로 하기 위해서다.
Ex) 31개의 데이터를 추가하기 위해서는.. 1 + 2 + 4 + 8 + 16 = ( 2^5 - 1 ) = 31 번의 연산이 필요
따라서, O(31/31) = O(1)의 평균 시간복잡도를 가진다!
- 만약, 재할당 규칙을 일정한 상수(M)으로 지정한다면... Add()메서드의 평균시간복잡도는 O(N)으로 계산될 수 있다.
언제 쓰는 것이 적합할까?
1. 많은 데이터가 선형적으로 이루어져 있을 때! --> add() : 시간복잡도 O(1)
2. 데이터의 직접적 접근(Get)이 자주 일어날 때! --> indexOf() : 시간복잡도 O(1)
- ArrayList의 메서드 시간복잡도를 생각하면 정말 쉽게 생각할 수 있다!!
- 자료의 추가, 접근에서 최고의 성능을 가진다. ( 상수 시간복잡도는 최고의 성능 )
이럴 땐 절대로 쓰지마
1. 자료의 중간 삽입이 필요할 때! --> add(index, val) : 시간복잡도 O(N)
2. 자료의 삭제가 빈번하게 일어날 때! --> remove(val or index) : 시간복잡도 O(N)
3. 자료를 직접적으로 검색할 때! --> contains() : 시간복잡도 O(N)
- 선형 자료구조라서, 값을 중간에 추가하거나 검색, 삭제할 때는 순차적으로 검색해야 된다!
- 따라서, 성능이 매우매우매우 저하된다. O(1) -> O(N) 이라니..
Ex) 데이터의 개수가 100만이면 1번의 연산에서 100만의 연산으로 바뀐다..
Vector와의 차이?
- ArrayList와 Vector는 동일한 구조를 갖는다.
- 다만, Vector는 자동 동기화를 보장하므로 멀티 쓰레드에서 안정적으로 사용이 가능하다.
- 그래서, 단일 쓰레드에서는 ArrayList가 성능이 더 좋다!!
소스코드 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
|
package dataStructure;
/**
* 자바의 대표 Collection Framework의 구성요소 중 하나인 ArrayList를 직접 구현한다.
* 원래, ArrayList Class의 경우 동적 배열이므로 원소 삽입시 2^n원소 마다 메모리를 할당받는 작업이 필요하다
* 그러한 과정은 생략하여 코드를 작성했다. ( 기존 배열의 size * 2배만큼 배열을 새로 할당하여, Arrays.copy 작업 진행 )
* @author huisam
*
*/
public class ArrayList {
/** 배열의 전체 사이즈를 나타낼 길이 */
private int length = 0;
/** 저장 배열을 나타낼 배열, 크기에 따라 사이즈를 늘리는 귀찮은 작업은 안했음 */
private int[] d = new int[1000];
/**
* 배열을 출력하는 함수
*/
public void print() {
if (isEmpty()) return;
System.out.print("(");
for (int i = 0; i < length - 1; i++)
System.out.print(d[i] + ", ");
System.out.println(d[length-1] + ")");
}
/**
* 배열이 비어있니?
* @return 비었으면 true, 아니면 false
*/
public boolean isEmpty() {
return length == 0 ? true : false;
}
/**
* 배열의 원소를 추가한다.
* 시간복잡도 O(1) , 메모리 재할당시 O(n) = A
* @param a
*/
public void add(int a) {
d[length++] = a;
}
/**
* 중간 삽입의 경우, 해당 위치에 원소를 삽입하고 뒤에 원소를 전부 밀어내야 하므로
* 맨앞에 놓는 최악의 경우 모든 원소를 한칸씩 뒤로 밀어내야 한다
* 시간복잡도 O(n)
* @param index 배열의 인덱스
* @param num 값
* @throws IndexOutOfBoundsException
*/
public void addIndexOf(int index, int num) throws IndexOutOfBoundsException {
if (get(index) == 0) throw new ArrayIndexOutOfBoundsException();
for (int i = length; i > index; i--) {
d[i] = d[i-1];
}
d[index] = num;
length++;
}
/**
* 배열의 크기를 리턴한다
* @return 배열의 크기
*/
public int size() {
return length;
}
/**
* 배열의 해당 원소를 리턴한다. 범위를 벗어나면 Exception발생
* get의 시간복잡도는 O(1)
* @param index
* @return d[index]
* @throws IndexOutOfBoundsException
*/
public int get(int index) throws IndexOutOfBoundsException {
if (isEmpty() || index >= length) throw new IndexOutOfBoundsException();
return d[index];
}
/**
* 배열의 해당 원소를 삭제한다. 범위를 벗어나면 Exception발생
* 보통의 삭제의 경우 배열의 크기를 축소하는 작업을 진행하기 때문에 모든 원소를 방문해야됨
* 시간복잡도는 O(N)
* @param index
* @throws IndexOutOfBoundsException
*/
public void remove(int index) {
if (isEmpty() || index >= length) throw new IndexOutOfBoundsException();
for(int i = index; i < length - 1; i++)
d[i] = d[i + 1];
d[--length] = 0;
}
/**
* 배열에 해당 원소가 있는지 검색하는 함수.
* 앞에서부터 순차적으로 검색하여 해당 원소를 포함하는지 여부를 조사한다.
* 최악의 경우 모든 원소를 검사하므로 시간복잡도는 O(n)
* @param num
* @return 찾으면 true, 없으면 false
*/
public boolean contains(int num) {
if (isEmpty()) return false;
for (int i = 0; i < length; i++) {
if (d[i] == num) {
return true;
}
}
return false;
}
public static void main(String[] args) {
ArrayList vec = new ArrayList();
vec.add(2);
vec.add(4);
vec.add(6);
vec.add(7);
vec.print();
vec.addIndexOf(2, 8);
vec.print();
vec.remove(3);
vec.print();
}
}
|
cs |
참고
[자료구조] 선형 자료 구조 - 1 (동적배열)
배열(Array)과 리스트(List)
'Developer > Data Structure' 카테고리의 다른 글
| Doubly Linked List - 이중 연결 리스트 (0) | 2019.11.10 |
|---|---|
| 자료구조 - HashTable(해쉬테이블), 해싱 (0) | 2019.04.30 |
| [ Collection Framework ] - 3. Priority Queue(우선순위큐) (2) | 2019.03.31 |
| [ Collection Framework ] - 1. 개요(컬렉션 프레임워크) (0) | 2019.03.31 |
