Hash?

- Hash Function : 해시 함수는 임의의 문자열을 받아서 고정 문자열로 바꾸어주는 함수다! 이때 서로 다른 문자열에 대하여 같은 고정 문자열이 될 수 있는데, 이러한 경우는 해쉬 충돌이라고 한다! H(s1) = H(s2)
- 따라서 많은 공간을 낭비하게 된다! Why? 해쉬 값이 어떻게 나올지 모르니까!
- 그럼에도 불구하고!! 우리는 메모리를 버리고 시간을 산 셈이다!
- 일반적으로 데이터를 조회할 때 배열은 O(n)이지만 잘 만든 Hash의 경우 O(1)의 조회가 가능하다
public int hashCode() {
int h = hash;
if (h == 0 && value.length > 0) {
char val[] = value;
for (int i = 0; i < value.length; i++) {
h = 31 * h + val[i];
}
hash = h;
}
return h;
}실제로 String Class의 hashCode 메서드
int hashKey(String data) {
int p = 1;
int key = 0;
for (int i = 0; i < data.length(); i++) {
key += data.charAt(i) * p;
p *= PN;
}
return ((key & 0x7fffffff) % TABLE_SIZE);
}작성자가 직접 구현한 HashCode()
- PN = PrimeNumber로 23을 사용했음
- key & 0x7ffffff 는 int 오버플로우시 양수로 변환하기 위한 작업
Hash Collision
- 서로 다른 문자열에 대해 HashCode()의 결과가 동일한 경우
- Hash Table을 구현할 대 충돌이 발생하면 Chaining 혹은 Open Addressing 으로 이를 해결한다!
Hash Table

- key value로 이루어진 한 쌍의 자료구조이다.
- 각각의 HashKey에 대하여 Buckets이라는 저장공간에 Mapping시키는 것이다!
- Table에서 제일 중요한 핵심은 동일한 Key 값에 대한 충돌을 어떻게 처리하느냐!!!
Chaining
- 충돌이 발생한 부분에 대하여 LinkedList로 삽입하여 문제를 해결한다!
- 찾고자 하는 Key값에 새로운 삽입이 발생하면 LinkedList로 앞(Head)에다 삽입하는 것이다!
- 다만 하나의 Key에 몰리게 되면 검색시 O(N)의 시간복잡도가 발생!
- 입력값을 예상할 수 없을 때와, 데이터가 적을 때 사용하는 방식이다.
- Java의 HashMap의 경우 Chaining 기법과 Double Hash 기법을 사용한 방식이다!

Open Addressing
- 일반적인 Table크기 만큼 배열을 가지고 저장한다!
- 동일한 Key값에 대해 충돌이 발생하면,, 다른 빈 key 주소로가서 저장하는 방식이다!
- 빈 주소를 찾는 방식에는 또 여러가지 방식이 있다!
1. Linear Probing(선형탐색)
- 현재 주소에서 고정 폭만큼 다음 주소로 비어있는 주소를 발견할 때까지 이동한다!

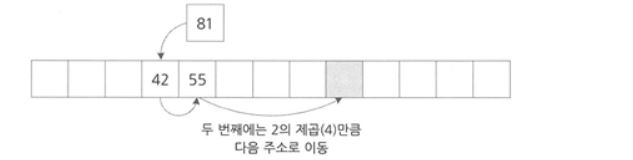
2. Quadratic Probing(제곱탐색)
- 선형탐사와 유사한데, 다만 이동폭이 제곱으로 늘어날 뿐이다!!
3. Double Hashing
- 2개의 해쉬 함수를 준비해서, 처음 해쉬 함수는 본래와 동일하고, 다른 하나는 충돌시 또 다른 주소를 얻어낸다!
int hashCode(int key) {
return key % 13;
}
int hashCode2(int key) {
return (key % 11) + 2;
}참고
c++에서 해시테이블 구현하기
Hash 함수, Hashing in Java
8장 해시 테이블
'Developer > Data Structure' 카테고리의 다른 글
| Doubly Linked List - 이중 연결 리스트 (0) | 2019.11.10 |
|---|---|
| [ Collection Framework ] - 3. Priority Queue(우선순위큐) (2) | 2019.03.31 |
| [ Collection Framework ] - 2. ArrayList(배열) (0) | 2019.03.31 |
| [ Collection Framework ] - 1. 개요(컬렉션 프레임워크) (0) | 2019.03.31 |
