반응형
MergeSort?
- 대표적인 분할정복 정렬 알고리즘 중의 하나
cf> 분할정복(Divide And Conquer) ? : 문제를 작은 2개의 문제로 분리하여, 해결하고 결과를 합치는 전략이다.
- 메모리를 잡아먹는 특징 때문에, 안정성이 많이 보장되는 정렬 알고리즘이다.
- 시간복잡도는 O(NlogN), 공간복잡도는 O(N) 이다.
++ 배열을 1개로 될 때까지 각각을 n/2로 줄이니 당연히 logN 이다.
++ 합칠 때는 총 N번의 비교연산이 들어가므로 N*logN 이 되는 시간복잡도이다!
- 보통 정렬의 공간복잡도는 O(1)인데, 병합정렬의 경우 복사할 배열이 새로 필요하다!

언제 써야될까?
1. 많은 데이터를 정렬할 때, 여분의 메모리가 충분할 때!
2. 반대로, 많은 데이터를 정렬하고 싶은데 메모리가 부족할 때!!!! --> 분할정복이 빛이 나게 된다
3. Quick정렬의 경우, 최악의 경우가 O(N^2)이므로 반드시 O(NlogN)으로 정렬하고 싶을 때!
정렬 과정
- 의외로 설명은 간단(?)하다.
1. 배열을 쪼개고 쪼개서 분할한다
2. 더 이상 쪼갤 수 없을 때, 왼쪽 파티션과 오른쪽 파티션을 정렬하여 합친다!
3. 이러한 작업을 원본 배열이 될 때까지 반복한다!!!


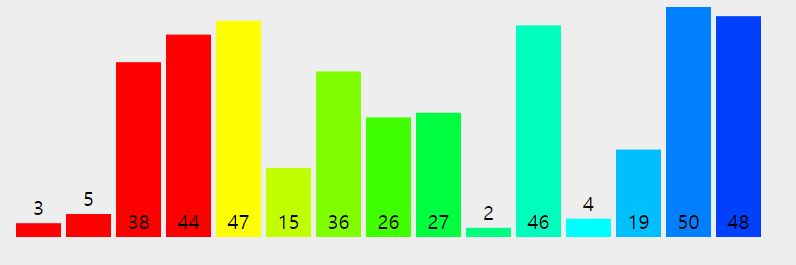
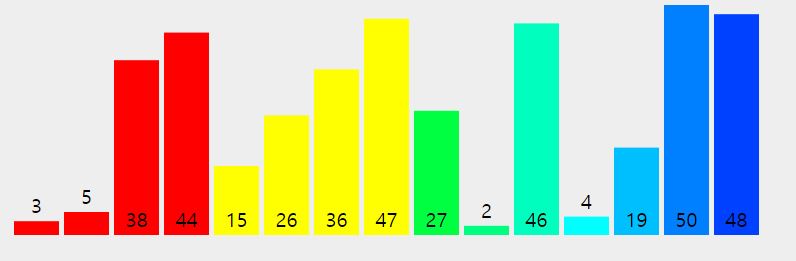

- 이러한 과정을 끝날 때까지 반복하면 정렬이 끝난다~!
코드 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
|
package dataStructure;
import java.util.Arrays;
/**
* [ 정렬 알고리즘 ] - Mergesort
* 시간복잡도 - O(NlogN) - 최악의 경우와 평균이 동일
* 공간복잡도 - O(N)
* 분할정복의 대표적인 알고리즘의 예시로, 시간복잡도가 항상 일정하기 유지된다는 것이 장점이다
* 배열을 나누고 임시배열을 또 따로 만들어야 하는 메모리 낭비가 있지만
* 안정적으로 이용할 수 있다는 것에 장점을 두고 있다.
* N이 1백만일 때, 79ms의 시간 소요가 된다!
* @author huisam
*
*/
public class MergeSort {
private static int SIZE = 1000000;
/** 배열을 저장할 변수 */
private int arr[] = new int[SIZE];
/** 정렬할 때 값을 저장할 임시 변수 */
private int sorted[] = new int[SIZE];
/** 객체 생성시 난수 뿌리기 */
public MergeSort() {
for (int i = 0; i < SIZE; i++) {
arr[i] = (int) (Math.random() * 100) + 1;
}
}
/**
* 배열을 출력할 메서드
*/
public void print() {
System.out.println(Arrays.toString(arr));
}
/**
* MergeSort 구현 메서드
* 1. 왼쪽과 오른쪽을 파티셔닝 한다.
* 2. 왼쪽 오른쪽을 나누었으면 정렬하면서 합친다!!
*/
public void mergeSort(int start, int end) {
if(start < end) {
int mid = (start + end) /2;
mergeSort(start, mid);
mergeSort(mid+ 1, end);
merge(start, mid, end);
}
}
/**
* 1.왼쪽 배열과 오른쪽 배열에 대하여 순차적으로 값을 비교한다!
* 2.더 작은 값이 있다면 임시 배열에 저장하고 인덱스를 늘린다
* 3.이러한 작업을 할 수 있을때 까지 반복한다!
* 4.마지막에 남은 배열에 모든 원소를 임시 배열에 붙인다!
* 5.최종적으로 임시배열을 원래 배열로 복사한다!
* @param start 왼쪽 배열의 시작
* @param mid 왼쪽 배열의 끝
* @param end 오른쪽 배열의 끝
*/
private void merge(int start, int mid, int end) {
int i = start; // 왼쪽 인덱스
int j = mid + 1; // 오른쪽 인덱스
int k = start; // 복사할 배열의 인덱스
while(i <= mid && j <= end) {
if(arr[i] <= arr[j])
sorted[k++] = arr[i++];
else
sorted[k++] = arr[j++];
}
if(mid < i) {
for (int l = j; l <= end; l++) {
sorted[k++] = arr[l];
}
}
else {
for (int l = i; l <= mid; l++) {
sorted[k++] = arr[l];
}
}
for (int l = start; l <= end; l++) {
arr[l] = sorted[l];
}
}
public static void main(String[] args) {
MergeSort ms = new MergeSort();
// ms.print();
long time = System.currentTimeMillis();
ms.mergeSort(0, 999999);
System.out.println("걸리는 시간 : " + (System.currentTimeMillis() - time) + "ms");
// ms.print();
}
}
|
cs |
참고
Sorting Algorithm을 비판적으로 바라보자
위키백과 - 합병정렬
반응형
'Developer > Algorithm' 카테고리의 다른 글
| [Path Algorithm] Bellman-Ford & SPFA (0) | 2019.05.01 |
|---|---|
| TopologicalSort - 위상정렬 (0) | 2019.04.19 |
| InsertionSort(삽입정렬)이란? (0) | 2019.04.05 |
| Quicksort(퀵정렬)이란? (0) | 2019.04.03 |
