반응형
위상정렬이란?
- DAG(Direct Acyclic Graph) 그래프에서 Node간의 정렬을 이루기 위해 사용하는 알고리즘
* DAG ? 방향성이 있고 사이클이 없는 그래프
- 그래프에 대한 모든 Node를 진입 차수가 짧은 순서대로 노드를 정리하는 방법이다.
- 진입차수가 0인 Node부터 순차적으로 검색하여, 최종적으로 제일 높은 진입차수가까지 정렬하는 방식

위상정렬 순서
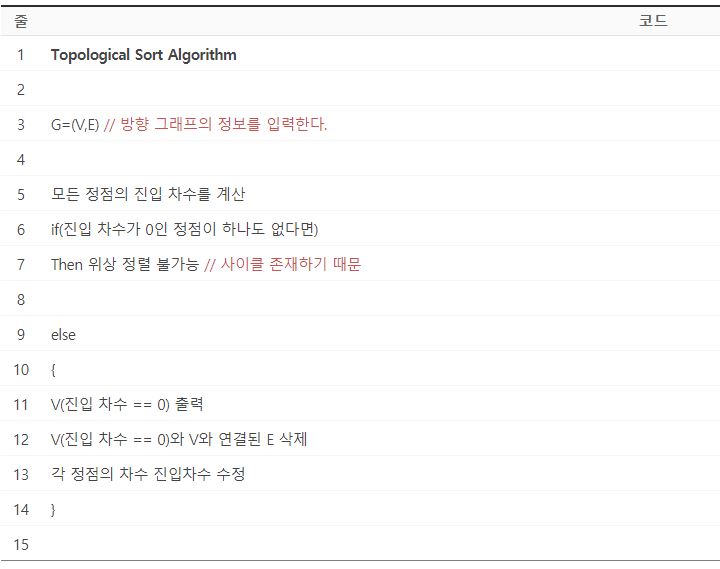
1. 인접 리스트 방식으로 그래프를 만들고, 노드별로 진입차수를 기록한다.
2. 큐를 2개 만든다. ( 로직이 진행되는 큐, 결과가 저장되는 큐 )
3. 진입 차수가 0인 Node들에 대하여 '탐색 큐'에 저장한다.
4. '탐색 큐'에서 Node를 하나씩 poll()을 한 뒤, 해당 Node를 '결과 큐'에 삽입한다.
5. '탐색 큐'에서 뽑은 Node에 대하여 다음 연결지점의 진입차수를 (-1) 한다.
6. 다음 Node지점에 대하여 진입차수가 0이라면 '탐색 큐'에 삽입한다.
7. 이 과정을 '탐색 큐'가 비었을 때까지 반복한다.
소스 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
|
import java.util.LinkedList;
import java.util.Queue;
/**
* 방향성이 있고 그래프가 없는 그래프(DAG)에서
* Node간의 순서를 정렬하기 위하여 사용되는 알고리즘
* 진입차수가 적은 것부터 시작해서 높은 순서대로 정렬된다!
* <p>
* Sample Data
* 1 -> 2
* 2 -> 5
* 3 -> 6
* 3 -> 7
* 4 -> 7
* 5 -> 8
* 6 -> 8
* 7 -> 8
*
* @author huisam
*/
class TopologicalSort {
private LinkedList<Integer>[] edge;
private int degree[];
private final int size = 10;
TopologicalSort() {
edge = new LinkedList[size];
for (int i = 0; i < size; i++) {
edge[i] = new LinkedList<>();
}
degree = new int[size];
makeData();
}
private void makeData() {
degree[2]++;
degree[5]++;
for (int i = 6; i < 8; i++) {
degree[i] = 2;
}
degree[8] = 3;
edge[1].push(2);
edge[2].push(5);
edge[2].push(6);
edge[3].push(6);
edge[3].push(7);
edge[4].push(7);
edge[5].push(8);
edge[6].push(8);
edge[7].push(8);
}
private void printResultQueue(Queue<Integer> resultQ) {
System.out.println("[위상정렬] 순서");
while (!resultQ.isEmpty()) {
System.out.print(resultQ.poll() + " ");
}
System.out.println();
}
private void sortStart() {
Queue<Integer> processQ = new LinkedList<>();
Queue<Integer> resultQ = new LinkedList<>();
// 진입차수가 0인것부터 시작한다.
for (int i = 0; i < size; i++) {
if (degree[i] == 0) {
processQ.add(i);
}
}
// 모든 노드를 방문할 떄 까지
while (!processQ.isEmpty()) {
int now = processQ.poll();
resultQ.add(now);
// 다음 방문 노드에 대해 하나씩 방문
for (int next : edge[now]) {
// 진입차수를 깍고
degree[next]--;
// 진입차수가 0이라면 진행한다.
if (degree[next] == 0) {
processQ.add(next);
}
}
}
printResultQueue(resultQ);
}
public static void main(String[] args) {
TopologicalSort topologicalSort = new TopologicalSort();
topologicalSort.sortStart();
}
}
|
cs |
* 시간복잡도 + 공간복잡도 고찰
- Queue를 2개 이용한 방식이니까 공간복잡도는 O(N^2 + 3N)이다.
= 최악의 경우 모든 Node가 서로 연결되어 있음 + degree배열 + Queue 2개
- 시간복잡도 O(N^2) 이다
= Node 하나에 대해서 모든 edge를 한번씩 탐색하므로, 2번 돌게 되는 것이다
참고
[그래프] 위상 정렬
위상 정렬 알고리즘
반응형
'Developer > Algorithm' 카테고리의 다른 글
| [Path Algorithm] Bellman-Ford & SPFA (0) | 2019.05.01 |
|---|---|
| InsertionSort(삽입정렬)이란? (0) | 2019.04.05 |
| Quicksort(퀵정렬)이란? (0) | 2019.04.03 |
| Mergesort(병합정렬)이란? (0) | 2019.04.01 |
